前面对选择排序,快速排序,希尔排序,归并排序,冒泡排序都进行了分析,最后一个是堆排序,刚开始实在不想写这个,感觉太麻烦了,无奈搜了一些面经,发现什么百度、腾讯、阿里等,他们都问到了堆排序,所以还是得认真聊一聊堆排序!
## 为什么要有堆排序?
堆非常典型的一个应用是优先队列,普通队列是先进先出,**优先队列则出队和入队无关,和他们各自的优先级有关!算法可以动态的选择优先级最高的任务执行!而任务的排序使用之前静态的排序方法是做不到的!**
**还有一个好处是,在N个元素里面选出前M个元素,用前面静态的方法,先排序再提取它的时间复杂度是nlogn,而使用优先队列它可以达到nlogM,把效率提高十几倍。**
优先队列正常的思维都是创建一个普通数组,入队时依次添加,出队时遍历一遍谁优先级最高,让它出队。
或者创建一个有序数组,入队的时候维护数组的有序性,这样出队就会按照优先级高低出队。
这两种方法都非常的好,但是都有其局限性,所以发明了第三种方法!(具体什么局限性俺也不知道,先继续往后看吧)
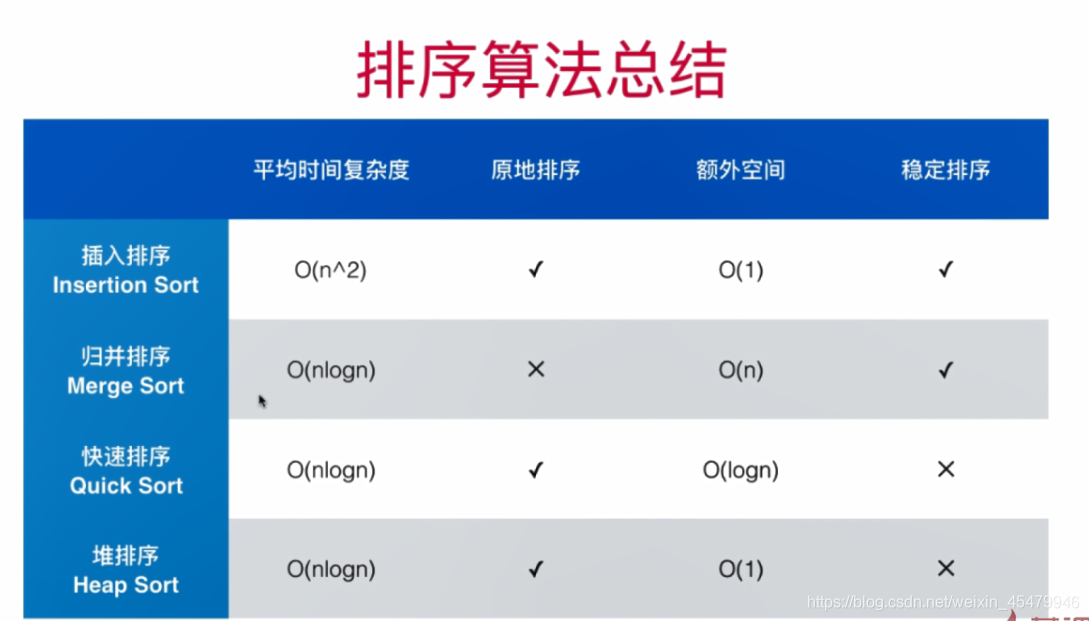
根据图片来看,堆虽然入队效率比普通数组差,出队效率比顺序数组差,但是平均下来效率却是三者中最好的!最差情况普通数组是O(n*n)级别,而堆是O(nlogn)级别。

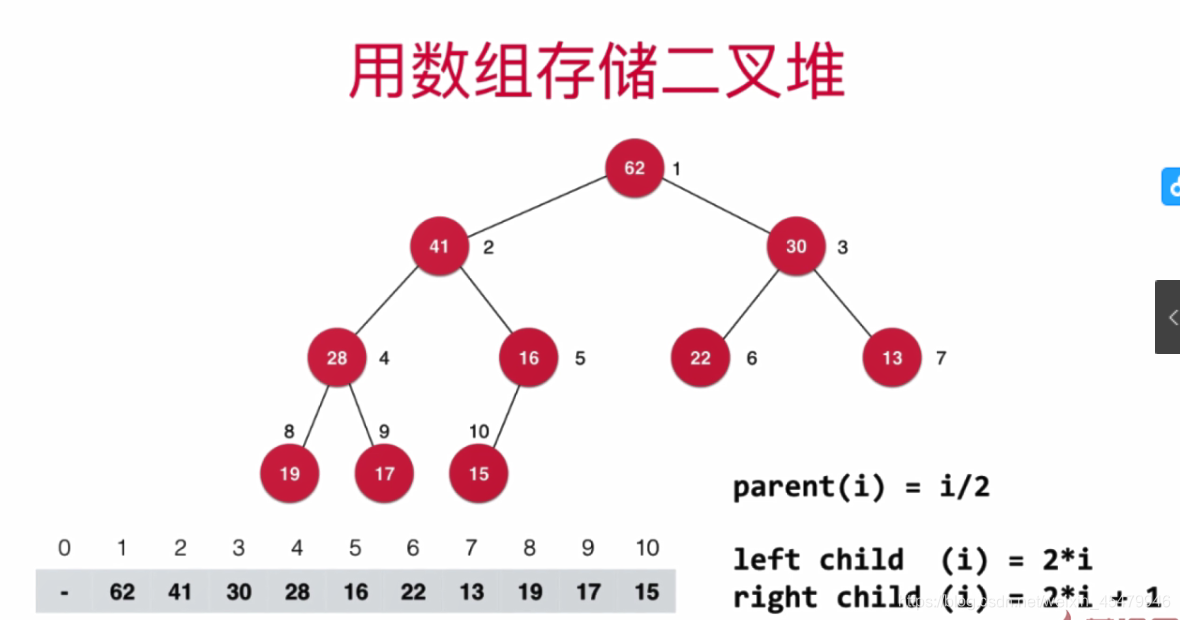
(二叉堆是一颗)完全二叉树:**除了最后一层外,其他层节点个数必须是最大值,并且叶子节点都要从最左边开始依次填满!**(只有完全二叉树才能用数组表示)
最大堆:父节点都不小于其子节点。
最小堆:父节点都不大于其子节点。
## 入队出队
给这个二叉树从上到下,从左往右标记一下顺序,就会发现,左孩子序号都是父亲序号?2,右孩子序号都是父亲序号?2+1.这样的话,入队的值放在最后,怎样保证它能调整到应有最大堆的位置呢?先让他和父节点进行比较,比父节点大就交换,然后依次往上对比,最后交换到自己的位置。
出队怎么出呢?出队就删除现在的根节点,然后把数组最后一个节点交换到根节点的位置,然后对它进行 “下沉”操作,即把它与其较大的那个子节点比大小,如果偏小就和子节点交换。
小插曲:在用Microsoft visiual C++ 进行编译的时候,一直跳出来说 “.exe无法解析的外部符号 _mainCRTStartup”错误。后来发现出错原因是自己建立的文件,其中的main函数并没有被编译,系统根本没有找到你的main函数,可能的原因是在其他地方创建的文件,没有被包含到项目里,解决办法就**是右击项目名称,重新创建一个你需要的文件。**
下面代码是**入队出队**的代码,最后以树的形式打印出来,并且保证树是最大堆。树形打印代码是复制粘贴修改后的,不用去记。
```cpp
#include<iostream>
using namespace std;//没有上面头文件std会报错!
#include<ctime>
#include<cassert>//等于#include<assert.h>
#include <algorithm>
#include <string>
#include <cmath>
template<typename Item>
class MaxHeap
{
private:
Item *data;//数组指针
int count;//数组元素个数
int capacity;
void shiftup(int k){
//如果该该节点值比父节点大,就把他俩交换一下,注意k>1!!
//!注意是while不是if!
while(k>1 && data[k/2]<data[k]){
swap(data[k/2],data[k]);
k/=2;
}
}
void shiftdown(int k){
//下沉的前提条件是必须要有孩子
while(2*k<=count){
int j=2*k;
//先比较两个子节点大小
if(data[j]<data[j+1] && j+1<=count){
j= j+1;
}
//遇到while循环就要先找到停止条件
if(data[k]>=data[j])//!if里的条件不是<!
break;
swap(data[k],data[j]);
k=j;//!不是k*2!
//下面这样写是错误的,如果父节点不小于子节点的情况下, 就不会跳出了,陷入死循环
//if(data[k]<data[j])//!if里的条件不是<!
//{
//swap(data[k],data[j]);
//k=j;//!不是k*2!
//}
}
//再跟父节点进行比较
}
public:
//构造函数
MaxHeap(int capacity){
//开辟一个临时数组
data=new Item[capacity+1];//!注意中括号前面的写法!
count = 0;//初始化元素个数
this->capacity = capacity;
}
~MaxHeap()
{
delete[] data;
}
int size()//获取元素个数
{
return count;
}
bool IsEmpty()
{
return count==0;
}
void Insert(Item item)//入队插入函数
{
assert(count+1<=capacity);//判断要放置的位置有没有越界
data[count+1] = item;//把新元素插入数组中
count++;//元素个数加1
shiftup(count);//把元素上移到对应位置,注意该函数放在私有位置,不对用户开放
}
int ExtractMax(){
assert(count>0);//取最大值的时候保证不是第0个
Item ret = data[1];
swap(data[1],data[count]);
count--;//取出来之后要记得减去
//对变化后的最大堆下沉之后,又会变成新的最大堆
shiftdown(1);
return ret;
}
public:
// 以树状打印整个堆结构
void testPrint(){
// 我们的testPrint只能打印100个元素以内的堆的树状信息
if( size() >= 100 ){
cout<<"This print function can only work for less than 100 int";
return;
}
// 我们的testPrint只能处理整数信息
if( typeid(Item) != typeid(int) ){
cout <<"This print function can only work for int item";
return;
}
cout<<"The max heap size is: "<<size()<<endl;
cout<<"Data in the max heap: ";
for( int i = 1 ; i <= size() ; i ++ ){
// 我们的testPrint要求堆中的所有整数在[0, 100)的范围内
assert( data[i] >= 0 && data[i] < 100 );
cout<<data[i]<<" ";
}
cout<<endl;
cout<<endl;
int n = size();
int max_level = 0;
int number_per_level = 1;
while( n > 0 ) {
max_level += 1;
n -= number_per_level;
number_per_level *= 2;
}
int max_level_number = int(pow(2.0, max_level-1));
int cur_tree_max_level_number = max_level_number;
int index = 1;
for( int level = 0 ; level < max_level ; level ++ ){
string line1 = string(max_level_number*3-1, ' ');
int cur_level_number = min(count-int(pow(2.0,level))+1,int(pow(2.0,level)));
bool isLeft = true;
for( int index_cur_level = 0 ; index_cur_level < cur_level_number ; index ++ , index_cur_level ++ ){
putNumberInLine( data[index] , line1 , index_cur_level , cur_tree_max_level_number*3-1 , isLeft );
isLeft = !isLeft;
}
cout<<line1<<endl;
if( level == max_level - 1 )
break;
string line2 = string(max_level_number*3-1, ' ');
for( int index_cur_level = 0 ; index_cur_level < cur_level_number ; index_cur_level ++ )
putBranchInLine( line2 , index_cur_level , cur_tree_max_level_number*3-1 );
cout<<line2<<endl;
cur_tree_max_level_number /= 2;
}
}
private:
void putNumberInLine( int num, string &line, int index_cur_level, int cur_tree_width, bool isLeft){
int sub_tree_width = (cur_tree_width - 1) / 2;
int offset = index_cur_level * (cur_tree_width+1) + sub_tree_width;
assert(offset + 1 < (int)line.size());
if( num >= 10 ) {
line[offset + 0] = '0' + num / 10;
line[offset + 1] = '0' + num % 10;
}
else{
if( isLeft)
line[offset + 0] = '0' + num;
else
line[offset + 1] = '0' + num;
}
}
void putBranchInLine( string &line, int index_cur_level, int cur_tree_width){
int sub_tree_width = (cur_tree_width - 1) / 2;
int sub_sub_tree_width = (sub_tree_width - 1) / 2;
int offset_left = index_cur_level * (cur_tree_width+1) + sub_sub_tree_width;
assert( offset_left + 1 < (int)line.size() );
int offset_right = index_cur_level * (cur_tree_width+1) + sub_tree_width + 1 + sub_sub_tree_width;
assert( offset_right < (int)line.size() );
line[offset_left + 1] = '/';
line[offset_right + 0] = '\\';
}
};
//int main()
//{
//MaxHeap<int> maxheap = MaxHeap<int>(100); //!创建带初始值堆的写法!
//srand((unsigned int)time(NULL));
//for(int i= 0; i<31; i++){
//maxheap.Insert(rand()%100);
//}
//
//maxheap.testPrint();
//while(!maxheap.IsEmpty()){
//cout<< maxheap.ExtractMax()<<" ";
//}
//while(1);
//return 0;
//}
```
## 1.出队入队堆排序
然后怎样利用这种堆的入队出队进行排序呢?你会发现这种**最大堆的根节点一定是数组中的最大值**,并且你每次取走根节点之后,又会把数组剩下的数中的最大值选出来放到根节点上,这样每次取出根节点就能进行排序了,下面是第一种排序的代码:
先把前面的入队出队程序放到heap1.h文件中,然后利用堆的函数进行排序。
```cpp
#include"Heap1.h"
template<typename T>
void heap_sort(T arr[], int n){
MaxHeap<int> maxheap = MaxHeap<int>(n); //!创建带初始值堆的写法!
for(int i= 0; i<n; i++){
maxheap.Insert(arr[i]);
}
for(int i= n-1; i>=0; i--){
arr[i]=maxheap.ExtractMax();
}
}
int main()
{
int n=7;
int arr[7]={7,5,10,4,2,3,0};
heap_sort(arr,n);
for(int k=0; k<n; k++)
{
//cout<<"排序后:"<<endl;
cout<<arr[k]<<" ";
}
while(1);
return 0;
}
```
## 2.heapify堆排序
上面是一种排序方法,还有一种排序方法不需要入队,直接在构造函数的地方进行数组内部的整理。它从第一个非叶子节点开始,第一个非叶子节点的求法是count/2,最大的元素个数除以2就是第一个非叶子节点,然后依次减减通过“下沉”把他们放到对应的位置,构成最大堆。
新的构造函数如下:
```cpp
MaxHeap(Item arr[],int n){
//开辟一个临时数组
data=new Item[n+1];//!这里算上第0个不占用的空间是n+1!
this->capacity = n;
for(int k=0;k<n;k++){
data[k+1]=arr[k];
}
count =n;//!元素个数要变化!!
//循环里是i--不是i/2
for(int i=count/2; i>0; i--){
shiftdown(i);
}
}
```
面向对象的调用函数如下:
```cpp
template<typename T>
void heap_sort2(T arr[], int n){
MaxHeap<T> maxheap = MaxHeap<T>(arr,n); //!创建带初始值堆的写法!
for(int i= n-1; i>=0; i--){
arr[i]=maxheap.ExtractMax();
}
}
```
最后同样可以进行排序。这种叫heapify排序方式。
**两种堆排序的区别在于:第一种就在初始构造函数中建了一个临时数组空间,然后靠往临时数组中插入和取出(或者说入队出队)得到最终有序数组。第二个heapify助排序是在构造函数里除了创建临时数组,还把所有元素放到临时数组中(注意临时数组第0位不放元素),并按照非叶子节点减减依次进行了排序。最后只需要依次取出堆顶元素即可。**
**一个插入的时候排序,一个全部放进去之后排序。一个面向对象要两个函数(插入取出)完成排序,一个面向对象只需要取出完成排序。第二种堆排序效果要好于第一种堆排序!**
将n个元素逐个插入到一个空堆中,算法复杂度是O(nlogn)
heapifty的过程,算法复杂度为O(n)
**排序仅仅是堆里面的一个小功能,堆最大的用处在于动态的数据维护!**
## 3.原始堆排序
原地堆排序是直接在原数组中先进行一波heapify助排序,但是原始数组并没有包含对第0个元素的处理,所以下沉的循环也变了,从2*k-1开始。
下沉排序的代码如下:
```cpp
// 原始的shiftDown过程
template<typename T>
//这里的k代表数组下标为k的非叶子节点
void __shiftDown(T arr[], int n, int k){
//几乎和shiftdown一样,不过是把2*k换成2*k+1,因为从0开始嘛
while( 2*k+1 < n ){
int j = 2*k+1;
if( j+1 < n && arr[j+1] > arr[j] )
j += 1;
if( arr[k] >= arr[j] )break;
swap( arr[k] , arr[j] );
k = j;
}
}
// 优化的shiftDown过程, 使用赋值的方式取代不断的swap,
// 该优化思想和我们之前对插入排序进行优化的思路是一致的
template<typename T>
void __shiftDown2(T arr[], int n, int k){
T e = arr[k];
while( 2*k+1 < n ){
int j = 2*k+1;
if( j+1 < n && arr[j+1] > arr[j] )
j += 1;
if( e >= arr[j] ) break;
arr[k] = arr[j];
k = j;
}
arr[k] = e;
}
```
最后一个元素的索引 = n-1,因为从0开始,用它求第一个非叶子节点也变成了(n-1-1)/2
在面向对象的函数中的使用:
```cpp
// 不使用一个额外的最大堆, 直接在原数组上进行原地的堆排序
template<typename T>
void heapSort(T arr[], int n){
// 注意,此时我们的堆是从0开始索引的
// 从(最后一个元素的索引-1)/2开始
// 最后一个元素的索引 = n-1,因为从0开始,用它求第一个非叶子节点也变成了(n-1-1)/2
//从第一个非叶子节点开始,对所有非叶子节点下沉之后,数组就会变成最大堆
for( int i = (n-1-1)/2 ; i >= 0 ; i -- )
__shiftDown2(arr, n, i);
//其实下面直接用提取函数就可以,但是因为不能借用其他数组
for( int i = n-1; i > 0 ; i-- ){
//把最大的数放到最后,就把它放在了正确的位置,
swap( arr[0] , arr[i] );
//对仅一次变化后的最大堆再进行下沉,又会变成新的最大堆
__shiftDown2(arr, i, 0);
}
}
```
## 部分排序算法对比
## 索引堆
上面建立的堆,如果看成一个个任务的话,有一个问题就是,要是想找出某一个任务不好找,因为他们的位置都在变动,每次必须从头遍历一下才能找到你需要的那个任务,这样太麻烦,于是就有人想出来,要不不要让任务变来变去,他们不动,让他们的替身,也就是用初始位置的编号作为一个索引,让这些索引代替原数值动。所以后面所有的最大堆,最大值都变成了索引,你想要知道原值是什么,把索引输进去作为编号就得到。于是产生了索引堆。
添加索引之后的代码如下:
/在下沉、上升、插入、删除的函数中,都要把以前的交换函数换成替代数组的交换函数,把条件比较换成index的下标
/然后
1.多了一个返回最大索引的函数、
2.多了一个根据索引返回用户值的函数
3.多了一个根据索引值修改任务值的函数
```cpp
#include<iostream>
using namespace std;//没有上面头文件std会报错!
#include<ctime>
#include<cassert>//等于#include<assert.h>
#include <algorithm>
#include <string>
#include <cmath>
//在下沉、上升、插入、删除的函数中,都要把以前的交换函数换成替代数组的交换函数,把条件比较换成index的下标
//然后1.还多了一个返回最大索引的函数 2.多了一个根据索引返回用户值的函数 3.多了一个根据索引值修改任务内容
template<typename Item>
class MaxHeap
{
private:
Item *data;//数组指针
Item *Index;
int count;//数组元素个数
int capacity;
void shiftup(int k){
//如果该该节点值比父节点大,就把他俩交换一下,注意k>1!!
//!注意是while不是if!
//比较还是比较原数组,但是交换就要换成替换数组
while(k>1 && data[Index[k/2]]<data[Index[k]]){
swap(Index[k/2],Index[k]);
k/=2;
}
}
void shiftdown(int k){
//下沉的前提条件是必须要有孩子
while(2*k<=count){
int j=2*k;
//先比较两个子节点大小
if(data[Index[j]]<data[Index[j+1]] && j+1<=count){
j= j+1;
}
//遇到while循环就要先找到停止条件
if(data[Index[k]]>=data[Index[j]])//!if里的条件不是<!
break;
swap(Index[k],Index[j]);
k=j;//!不是k*2!
//下面这样写是错误的,如果父节点不小于子节点的情况下, 就不会跳出了,陷入死循环
//if(data[k]<data[j])//!if里的条件不是<!
//{
//swap(data[k],data[j]);
//k=j;//!不是k*2!
//}
}
//再跟父节点进行比较
}
public:
//构造函数
MaxHeap(int capacity){
//开辟一个临时数组
data=new Item[capacity+1];//!注意中括号前面的写法!
Index=new Item[capacity+1];
count = 0;//初始化元素个数
this->capacity = capacity;
}
MaxHeap(Item arr[],int n){
//开辟一个临时数组
data=new Item[n+1];//!这里算上第0个不占用的空间是n+1!
this->capacity = n;
for(int k=0;k<n;k++){
data[k+1]=arr[k];
}
count =n;//!元素个数要变化!!
//循环里是i--不是i/2
for(int i=count/2; i>0; i--){
shiftdown(i);
}
}
~MaxHeap()
{
delete[] data;
delete[] Index;
}
int size()//获取元素个数
{
return count;
}
bool IsEmpty()
{
return count==0;
}
void Insert(int i,Item item)//入队插入函数
{
assert(count+1<=capacity);//判断要放置的位置有没有越界
assert(i>=1 && i<=capacity);
//替代数组Index在末尾加上添加的下标
//真正的数组就在在另一个数组新下标下面添加上对应的值
i+=1;
Index[count+1]=i;
data[i] = item;//把新元素插入数组中
count++;//元素个数加1
shiftup(count);//把元素上移到对应位置,注意该函数放在私有位置,不对用户开放
}
int ExtractMax(){
assert(count>0);//取最大值的时候保证不是第0个
Item ret = data[Index[1]];
swap(Index[1],Index[count]);
count--;//取出来之后要记得减去
shiftdown(1);
return ret;
}
//返回最大索引
int Index_ExtractMax(){
assert(count>0);//取最大值的时候保证不是第0个
int ret = Index[1]-1;//最大索引要减一,因为从外部来看是从0开始的
swap(Index[1],Index[count]);
count--;//取出来之后要记得减去
shiftdown(1);
return ret;
}
//返回索引对应用户值
Item getItem(int i){
return data[i+1];//对用户来说是从0开始的
}
//改变用户的值
void change(int i, Item newItem){
i+=1;
data[i]=newItem;
//找到替身数组中对应的下标值,然后
if(int j=0;j<count;j++){
if(Index[j]==i){
//我刚开始觉得下面得操作多此一举,替身数组得下标又没有改变,没必要挪动他们得位置
//后来明白了,原数组变了,替身的位置是一定要变得!下沉上升操作都是针对原数组的,替身在上升下沉的过程中只是作为下标的存在。
shiftdown(j);
shiftup(j);
return;
}
}
}
public:
// 以树状打印整个堆结构
void testPrint(){
// 我们的testPrint只能打印100个元素以内的堆的树状信息
if( size() >= 100 ){
cout<<"This print function can only work for less than 100 int";
return;
}
// 我们的testPrint只能处理整数信息
if( typeid(Item) != typeid(int) ){
cout <<"This print function can only work for int item";
return;
}
cout<<"The max heap size is: "<<size()<<endl;
cout<<"Data in the max heap: ";
for( int i = 1 ; i <= size() ; i ++ ){
// 我们的testPrint要求堆中的所有整数在[0, 100)的范围内
assert( data[i] >= 0 && data[i] < 100 );
cout<<data[i]<<" ";
}
cout<<endl;
cout<<endl;
int n = size();
int max_level = 0;
int number_per_level = 1;
while( n > 0 ) {
max_level += 1;
n -= number_per_level;
number_per_level *= 2;
}
int max_level_number = int(pow(2.0, max_level-1));
int cur_tree_max_level_number = max_level_number;
int index = 1;
for( int level = 0 ; level < max_level ; level ++ ){
string line1 = string(max_level_number*3-1, ' ');
int cur_level_number = min(count-int(pow(2.0,level))+1,int(pow(2.0,level)));
bool isLeft = true;
for( int index_cur_level = 0 ; index_cur_level < cur_level_number ; index ++ , index_cur_level ++ ){
putNumberInLine( data[index] , line1 , index_cur_level , cur_tree_max_level_number*3-1 , isLeft );
isLeft = !isLeft;
}
cout<<line1<<endl;
if( level == max_level - 1 )
break;
string line2 = string(max_level_number*3-1, ' ');
for( int index_cur_level = 0 ; index_cur_level < cur_level_number ; index_cur_level ++ )
putBranchInLine( line2 , index_cur_level , cur_tree_max_level_number*3-1 );
cout<<line2<<endl;
cur_tree_max_level_number /= 2;
}
}
private:
void putNumberInLine( int num, string &line, int index_cur_level, int cur_tree_width, bool isLeft){
int sub_tree_width = (cur_tree_width - 1) / 2;
int offset = index_cur_level * (cur_tree_width+1) + sub_tree_width;
assert(offset + 1 < (int)line.size());
if( num >= 10 ) {
line[offset + 0] = '0' + num / 10;
line[offset + 1] = '0' + num % 10;
}
else{
if( isLeft)
line[offset + 0] = '0' + num;
else
line[offset + 1] = '0' + num;
}
}
void putBranchInLine( string &line, int index_cur_level, int cur_tree_width){
int sub_tree_width = (cur_tree_width - 1) / 2;
int sub_sub_tree_width = (sub_tree_width - 1) / 2;
int offset_left = index_cur_level * (cur_tree_width+1) + sub_sub_tree_width;
assert( offset_left + 1 < (int)line.size() );
int offset_right = index_cur_level * (cur_tree_width+1) + sub_tree_width + 1 + sub_sub_tree_width;
assert( offset_right < (int)line.size() );
line[offset_left + 1] = '/';
line[offset_right + 0] = '\\';
}
};
//int main()
//{
//MaxHeap<int> maxheap = MaxHeap<int>(100); //!创建带初始值堆的写法!
//srand((unsigned int)time(NULL));
//for(int i= 0; i<31; i++){
//maxheap.Insert(rand()%100);
//}
//
//maxheap.testPrint();
//while(!maxheap.IsEmpty()){
//cout<< maxheap.ExtractMax()<<" ";
//}
//while(1);
//return 0;
//}
```
## 堆索引堆的优化
添加一个反向数组,里面保存每一个下标(除了0)在替身中的位置。
有如下特性:

代码中对每一次替身的交换都进行了反向数组的优化交换,最终实现对修改堆中数值函数的时间优化,让它从O(n*n)变成了O(1)。
```cpp
#include<iostream>
using namespace std;//没有上面头文件std会报错!
#include<ctime>
#include<cassert>//等于#include<assert.h>
#include <algorithm>
#include <string>
#include <cmath>
//在下沉、上升、插入、删除的函数中,都要把以前的交换函数换成替代数组的交换函数,把条件比较换成index的下标
//然后1.还多了一个返回最大索引的函数 2.多了一个根据索引返回用户值的函数 3.多了一个根据索引值修改任务内容
template<typename Item>
class MaxHeap
{
private:
Item *data;//数组指针
Item *Index;
Item *rev;
int count;//数组元素个数
int capacity;
void shiftup(int k){
//如果该该节点值比父节点大,就把他俩交换一下,注意k>1!!
//!注意是while不是if!
//比较还是比较原数组,但是交换就要换成替换数组
while(k>1 && data[Index[k/2]]<data[Index[k]]){
swap(Index[k/2],Index[k]);
k/=2;
}
}
void shiftdown(int k){
//下沉的前提条件是必须要有孩子
while(2*k<=count){
int j=2*k;
//先比较两个子节点大小
if(data[Index[j]]<data[Index[j+1]] && j+1<=count){
j= j+1;
}
//遇到while循环就要先找到停止条件
if(data[Index[k]]>=data[Index[j]])//!if里的条件不是<!
break;
swap(Index[k],Index[j]);
rev[Index[k]] = k;
rev[Index[j]] = j;
k=j;//!不是k*2!
//下面这样写是错误的,如果父节点不小于子节点的情况下, 就不会跳出了,陷入死循环
//if(data[k]<data[j])//!if里的条件不是<!
//{
//swap(data[k],data[j]);
//k=j;//!不是k*2!
//}
}
//再跟父节点进行比较
}
public:
//构造函数
MaxHeap(int capacity){
//开辟一个临时数组
data=new Item[capacity+1];//!注意中括号前面的写法!
Index=new Item[capacity+1];
rev =new Item[capacity+1];
count = 0;//初始化元素个数
this->capacity = capacity;
}
MaxHeap(Item arr[],int n){
//开辟一个临时数组
data=new Item[n+1];//!这里算上第0个不占用的空间是n+1!
this->capacity = n;
for(int k=0;k<n;k++){
data[k+1]=arr[k];
}
count =n;//!元素个数要变化!!
//循环里是i--不是i/2
for(int i=count/2; i>0; i--){
shiftdown(i);
}
}
~MaxHeap()
{
delete[] data;
delete[] Index;
delete[] rev;
}
int size()//获取元素个数
{
return count;
}
bool IsEmpty()
{
return count==0;
}
void Insert(int i,Item item)//入队插入函数
{
assert(count+1<=capacity);//判断要放置的位置有没有越界
assert(i>=1 && i<=capacity);
//替代数组Index在末尾加上添加的下标
//真正的数组就在在另一个数组新下标下面添加上对应的值
i+=1;
Index[count+1]=i;
rev[i]=count+1;//优化
data[i] = item;//把新元素插入数组中
count++;//元素个数加1
shiftup(count);//把元素上移到对应位置,注意该函数放在私有位置,不对用户开放
}
int ExtractMax(){
assert(count>0);//取最大值的时候保证不是第0个
Item ret = data[Index[1]];
swap(Index[1],Index[count]);
//优化
rev[Index[1]] = 1;
rev[Index[count]] = 0;//这里有点晕!!!
count--;//取出来之后要记得减去
shiftdown(1);
return ret;
}
//返回最大索引
int Index_ExtractMax(){
assert(count>0);//取最大值的时候保证不是第0个
int ret = Index[1]-1;//最大索引要减一,因为从外部来看是从0开始的
swap(Index[1],Index[count]);
//优化
rev[Index[1]] = 1;
rev[Index[count]] = 0;//因为要把这个对应的元素删除
count--;//取出来之后要记得减去
shiftdown(1);
return ret;
}
bool contain(int i){
assert(i+1>=1 && i+1<=capacity);
return rev[i+1]!=0;//只有下标不在替身数组的时候才为0
}
//返回索引对应用户值
Item getItem(int i){
assert(contain(i));//为了保证这个i在替身数组中
return data[i+1];//对用户来说是从0开始的
}
//改变用户的值
void change(int i, Item newItem){
assert(contain(i));
i+=1;
data[i]=newItem;
//找到替身数组中对应的下标值,然后
//if(int j=0;j<count;j++){
//if(Index[j]==i){
int j=rev[i];
//我刚开始觉得下面得操作多此一举,替身数组得下标又没有改变,没必要挪动他们得位置
//后来明白了,原数组变了,替身的位置是一定要变得!下沉上升操作都是针对原数组的,替身在上升下沉的过程中只是作为下标的存在。
shiftdown(j);
shiftup(j);
return;
//}
//}
}
public:
// 以树状打印整个堆结构
void testPrint(){
// 我们的testPrint只能打印100个元素以内的堆的树状信息
if( size() >= 100 ){
cout<<"This print function can only work for less than 100 int";
return;
}
// 我们的testPrint只能处理整数信息
if( typeid(Item) != typeid(int) ){
cout <<"This print function can only work for int item";
return;
}
cout<<"The max heap size is: "<<size()<<endl;
cout<<"Data in the max heap: ";
for( int i = 1 ; i <= size() ; i ++ ){
// 我们的testPrint要求堆中的所有整数在[0, 100)的范围内
assert( data[i] >= 0 && data[i] < 100 );
cout<<data[i]<<" ";
}
cout<<endl;
cout<<endl;
int n = size();
int max_level = 0;
int number_per_level = 1;
while( n > 0 ) {
max_level += 1;
n -= number_per_level;
number_per_level *= 2;
}
int max_level_number = int(pow(2.0, max_level-1));
int cur_tree_max_level_number = max_level_number;
int index = 1;
for( int level = 0 ; level < max_level ; level ++ ){
string line1 = string(max_level_number*3-1, ' ');
int cur_level_number = min(count-int(pow(2.0,level))+1,int(pow(2.0,level)));
bool isLeft = true;
for( int index_cur_level = 0 ; index_cur_level < cur_level_number ; index ++ , index_cur_level ++ ){
putNumberInLine( data[index] , line1 , index_cur_level , cur_tree_max_level_number*3-1 , isLeft );
isLeft = !isLeft;
}
cout<<line1<<endl;
if( level == max_level - 1 )
break;
string line2 = string(max_level_number*3-1, ' ');
for( int index_cur_level = 0 ; index_cur_level < cur_level_number ; index_cur_level ++ )
putBranchInLine( line2 , index_cur_level , cur_tree_max_level_number*3-1 );
cout<<line2<<endl;
cur_tree_max_level_number /= 2;
}
}
private:
void putNumberInLine( int num, string &line, int index_cur_level, int cur_tree_width, bool isLeft){
int sub_tree_width = (cur_tree_width - 1) / 2;
int offset = index_cur_level * (cur_tree_width+1) + sub_tree_width;
assert(offset + 1 < (int)line.size());
if( num >= 10 ) {
line[offset + 0] = '0' + num / 10;
line[offset + 1] = '0' + num % 10;
}
else{
if( isLeft)
line[offset + 0] = '0' + num;
else
line[offset + 1] = '0' + num;
}
}
void putBranchInLine( string &line, int index_cur_level, int cur_tree_width){
int sub_tree_width = (cur_tree_width - 1) / 2;
int sub_sub_tree_width = (sub_tree_width - 1) / 2;
int offset_left = index_cur_level * (cur_tree_width+1) + sub_sub_tree_width;
assert( offset_left + 1 < (int)line.size() );
int offset_right = index_cur_level * (cur_tree_width+1) + sub_tree_width + 1 + sub_sub_tree_width;
assert( offset_right < (int)line.size() );
line[offset_left + 1] = '/';
line[offset_right + 0] = '\\';
}
};
//int main()
//{
//MaxHeap<int> maxheap = MaxHeap<int>(100); //!创建带初始值堆的写法!
//srand((unsigned int)time(NULL));
//for(int i= 0; i<31; i++){
//maxheap.Insert(rand()%100);
//}
//
//maxheap.testPrint();
//while(!maxheap.IsEmpty()){
//cout<< maxheap.ExtractMax()<<" ";
//}
//while(1);
//return 0;
//}
```
上述所有的就是优先队列,可以用于游戏设计,排序,归并排序的多路排序等很多地方。